Get started with Ory Permissions
Ory Permissions (based on Ory Keto) implements Google Zanzibar. This document explains the most fundamental concepts necessary to work with Ory Permissions and gives you an opportunity to create and query a simple set of relationships.
Basic concepts
Before you start, learn about the basic concepts used in Ory Permissions.
Relations and relationships
The data model used by Ory Permissions are so-called relationships that encode relations between subjects and objects.
Examples of relationships are:
users:user1 is in members of groups:group1
members of groups:group1 are readers of files:file1
As you can see, the subject of a relationship can either be a specific subject ID, or subjects defined through an indirection (all members of a certain group). The object is referenced by its ID.
Checking permissions
Permissions are just another form of relations. Therefore, a permission check is a request to check whether a subject has a certain relation to an object, possibly through one or more indirections.
As a very simple example, let's assume the following tuples exist:
users:user1 is in members of groups:group1
members of groups:group1 are readers of files:file1
Based on these tuples, you can run permission checks:
-
Is
user1areaderoffile1?// YesYes, because
user1is inmembersofgroups:group1and allmembersofgroups:group1arereadersoffiles:file1. -
Is
user2a member ofgroup1?// NoNo, because there is no relation between
user2andgroup1.
Example
This example setup demonstrates the basics of relationship management and usage of the Check API.
This guide explains how to configure namespaces and relationship rules using the Ory Permission Language (OPL). You can then run fine-grained checks against Ory Permissions, which are answered based on a combination of OPL and the concrete high-level relationships stored.
The example describes a file store. Individual files are organized in a folder hierarchy, and can be accessed by individual users or groups of users. Using the Ory Permission Language you can specify that if a user has access to a folder, the user also has access to all files in that folder.
Ory Network setup
The fastest way to get started with Ory Permissions is using Ory Console.
Go to Permissions → Relationships in the Ory Console and switch to the Permission Rules tab.
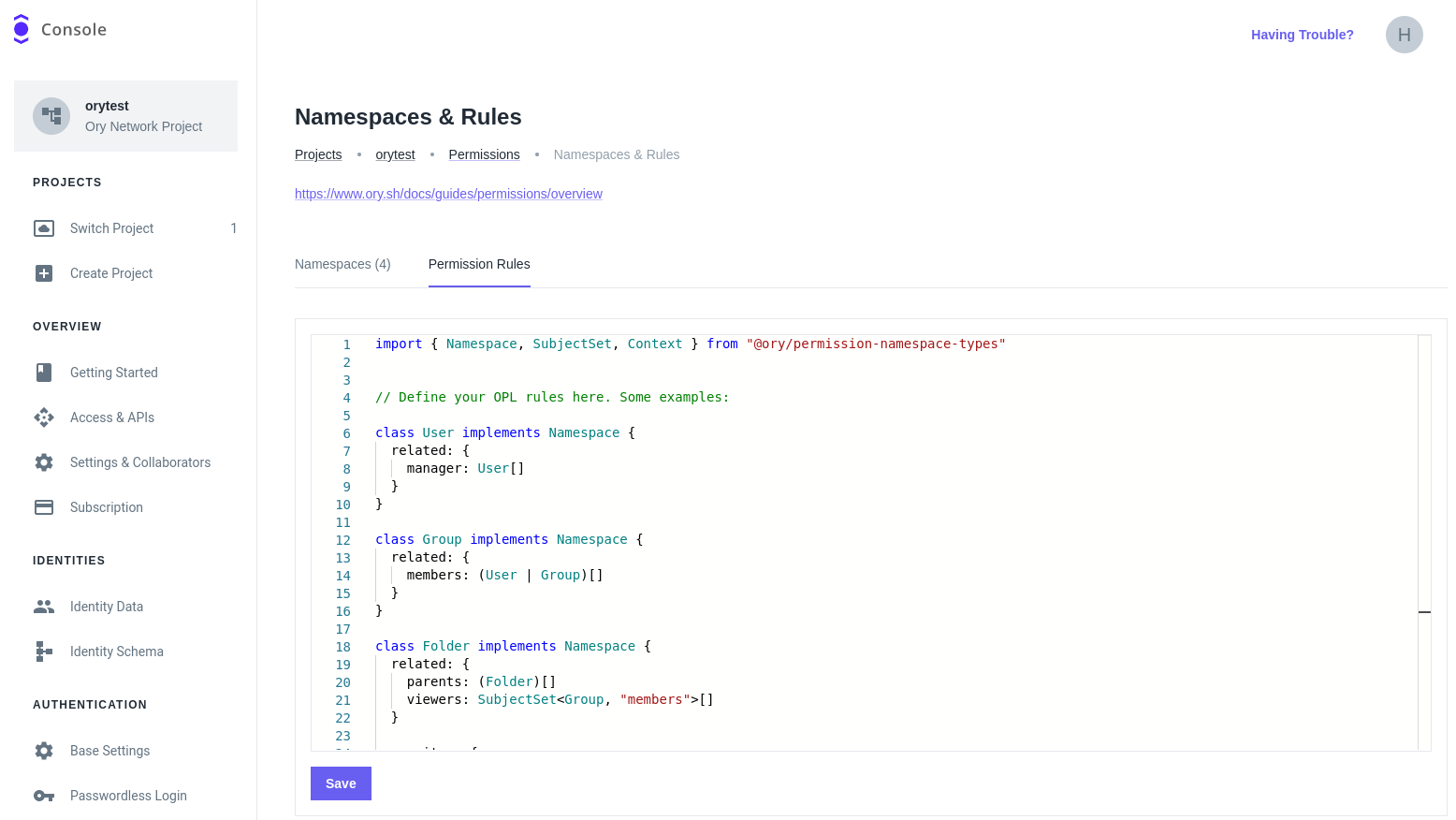
Paste the following content into the editor:
The editor offers autocompletion for the Ory Permission Language.
Connecting to Ory Network via CLI
Next, connect to the Ory Network using the Ory CLI. If you haven't done so already, install the Ory CLI.
Follow these steps:
-
Sign in to your Ory Network account:
ory auth -
List your workspaces and projects:
ory list workspaces
ory list projects --workspace <workspace-id> -
Use the project ID of the project in which you want to create permission rules:
ory use project <project-id>
Creating relationships
Next, create relationships in your Ory Network project using the Ory CLI.
The following relationships showcase the namespace configuration. The sample defines a developer group with two members and a
folder hierarchy. Through the rules in the Ory Permission Language, every member of the developer group can access the files in
the hierarchy.
You can create additional fine-grained permission rules for certain objects, similar to the private file.
Save the file as relationships.json in your current working directory. To create these relationships in Ory Permissions, run
this command:
ory create relationships relationships.json
# Output:
# NAMESPACE OBJECT RELATION NAME SUBJECT
# Group developer members patrik
# Group developer members User:Patrik
# Group developer members User:Henning
# Folder keto/ viewers Group:developer#members
# File keto/README.md parents Folder:keto/
# Folder keto/src/ parents Folder:keto/
# File keto/src/main.go parents Folder:keto/src/
# File private owners User:Henning
Checking for permissions
With the relationships created, try running queries that illustrate use cases:
Transitive permissions for objects in the hierarchy
Patrik can view keto/src/main.go. This file is in the keto/src folder, which is in keto. The keto directory has the
"developer" group as its "viewers". Patrik is a member of the "developer" group.
ory is allowed User:Patrik view File keto/src/main.go
Allowed
No transitivity for objects outside the hierarchy
Patrik cannot view the private file, since that file is not part of any folder hierarchy Patrik has access to.
ory is allowed User:Patrik view File private
Denied
Fine-grained permissions for any object
Henning can both edit and view the private file, since he is an "owner" of it.
ory is allowed User:Henning view File private
Allowed
ory is allowed User:Henning edit File private
Allowed
Next steps
- Learn what a permission model is and how to create one.
- Read the Ory Permission Language specification.